Context
As described earlier, we could operate the reactor in
three different ways
- Using a pH/CO2 controller for CO2 injection and stability
- Using a precision CO2 regulator to precisely adjust CO2 injection
- Overflow mode.
Most current users are either using a pH/CO2 controller or a precision CO2 regulator. There will be a reservoir of almost pure CO2 gas in the reactor, and the physics/chemistry of CO2 absorption into the water will be similar to any other reactor that may or may not use CO2 bubbles. As is also the case in bubble reactors, gradually we will see some oxygen and nitrogen outgas from the tank water into the pure CO2 pocket in the reactor (Henry’s law), but with an occasional manual purge this is not detrimental to the absorption of the injected CO2. The CO2 is stabilised by the pH/CO2 controller, or the regulator, so we’re all good. With the various users now having success with the reactor we might conclude that we understand it well enough, but doing so we may miss the opportunity to explore the pro’s and con’s of overflow mode.
My favourite mode of operation is the overflow mode, and I’ve been using it previously with CO2 Spray Bar as well. Even though I am generally a fan of pH/CO2 controllers, I decided to not buy a new one when my controller broke down a few months ago. I really like the simplicity of the reactor in overflow mode, no need to handle pH probes, calibration, dKH, and no need to invest in a pricey CO2 regulator. The future will tell if and when other users will buy in to it, or that for whatever reason we will stick with controllers and regulators and use the reactor in a more conventional way.
In this post in share some measurements and calculations to better understand overflow mode. This is not a forum for math, fortunately, but I do believe it is helpful to document insights, so that anyone interested can verify and perhaps build further on these ideas. Please accept my apology, and I hope it is appreciated that the most disturbing part with the calculations is hidden in the attached file
 The model for the reactor in overflow mode
View attachment 3186
The model for the reactor in overflow mode
View attachment 3186
For the model we assume a ‘steady state’, i.e. all physical properties are stabilised and no longer changing in time.
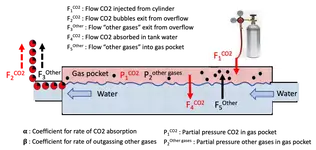
We inject pure CO2 from the cylinder into the reactor, (F1), and each CO2 molecule is either absorbed into the water flow (F4), or exits in a bubble from the overflow (F2). We assume that the flow F4 is proportional to the partial pressure P1 of CO2 in the gas pocket: F4 = Alpha P1. The linear relationship is a reasonable assumption as the concentration of CO2 in the tank (typically 30 ppm) is far below the CO2 saturation level in pure water (>1000 ppm at room temperature)
“Other gases” (O2, N2, …) in the tank water will aim for equilibrium with the gas pocket in the reactor (Henry’s law). As we are injecting pure CO2 in the reactor, with atmospheric pressure, we can assume that the partial pressure P2 of “other gases” is low, and a linear relationship F5 = Beta P1. This flow F5 is much smaller than F4 (see below measurement) therefore the fraction of other gases in the pocket will slowly grow, until the upper half of the reactor is full and bubbles start to purge from the exit and the reactor can go to steady state overflow mode where F3 = F5
For all model calculations we scale the gas flows with Alpha, that is F1/Alpha, F2/Alpha, F3/Alpha, F4/Alpha, F5/Alpha, so that the conclusions can be applied to any size of reactor without further corrections.
F1/Alpha = 1 is an important reference point for the interpretation of the calculations. It corresponds to the CO2 flow into the reactor, when the reactor has just been purged, then fully filled with pure CO2, and the F1 flow maximized to the level where the overflow just starts to purge. In this case F1 = F4 = Alpha P1 = Alpha.
An important parameter in the model is the ratio Beta/Alpha, which tells us how the ‘other gases’ outgas from the water into the gas pocket, compared to the absorption of CO2 into the water.
Measurement of Beta/Alpha
A container (‘Horizontal reactor’) filled with 2 litre CO2, placed upside down in a bathtub. Gyre created some surface agitation and a waterflow under the CO2 gas pocket. 2/3 of the gas pocket was gone after 1 hour, and taken measurement after 2 hours when pocket seemed not to shrink much anymore. Used a pipette to suck the remaining gas from the container, and transferred it to a measurement cup that was held upside down under the water to have a precise measurement of the gas volume.
Estimated Beta/Alpha = 60 ml / 2000 ml = 3%.
View attachment 3188
Model results
The mathematics to calculate the flows as a function of the CO2 injection are in the attached file. I will not elaborate on that, the interested reader (if any

) will notice that the math is really basic, but I rather try to give an intuitive explanation what it all means.
View attachment 3189
On the horizontal axis we have F1/Alpha, remember that F1/Alpha =1 corresponds to the flow when the reactor is full with pure CO2, and the overflow is just starting to show the first bubbles purging. The curves are F2/Alpha (CO2 purging as bubbles from the exit tube), F3/Alpha and F5/Alpha (the flows of other gases, which are relatively low), as well as F4/Alpha (the flow of CO2 being injected into the tank water).
At high F1/Alpha, we see that the F4/Alpha approaches 1 and does not change anymore. This corresponds to a reactor that is blown with plenty CO2, so that the gas pocket is nearly pure CO2 and the injection F4/Alpha is constant. In this situation any additional volume of CO2 that is pushed into the reactor goes straight out as losses with F2 purging – hence the blue curve approaching this straight line upwards. But, we have a nearly perfectly stable CO2 injection.
At really low F1/Alpha we see that the purging stops, but also that the CO2 injected into the water (F4/Alpha) is strongly dependent on the rate of injection (F1/Alpha), and indeed this is the situation where the reactor is not in overflow mode and would need a pH/CO2 controller or precision CO2 regulator to stabilise the tank.
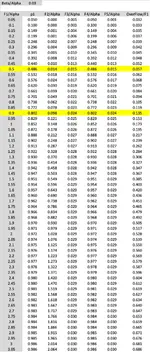
Settings for overflow mode
Refer to this table
View attachment 3190
In case that we have plenty of CO2 available, and don’t care too much about CO2 losses, it could work to inject plenty of flow (perhaps at F1/Alpha = 2), and with that F4/Alpha will always be very close to 1. Variations in F1 injection (unstable, low quality CO2 regulator) will hardly have any effect on the CO2 injection.
When looking for a compromise between CO2 consumption and stability then a sweet spot could be at F1/Alpha = 1. We can read from the table that CO2 purging is then only 15%. When we then would apply variations of 10% up and 10% down on F1/Alpha, we see that this total 20% variation only gives 10% variation for the F4 flow that gets injected in the water.
If we want to trade more stability for more CO2 consumption, just increase the injected flow above F1/Alpha = 1.
In summary, how do I now set up my reactor in overflow mode?
After each weekly maintenance and water change I purge my reactor, and turn solenoid on. The reactor will fill with pure CO2, as the flow of other gases is just 3% of the CO2 flow. When the reactor is full, I slowly dial my injection down until the point that the reactor stops purging bubbles. This is my F1/Alpha =1 “sweet spot”. If later during the week my regulator will drift by X%, I know that my injected CO2 will only change by X/2%. I do not need a pH/CO2 controller, nor a really precision CO2 regulator for this, as it is my reactor geometry that helps me to stabilise my tank, and indeed at very limited CO2 consumption.
As I believe that CO2 stability matters more for the plants than the absolute level (30 or 40 ppm, what is really the impact), I consider to shorten my reactor a bit, have slightly less CO2 ppm but at an even higher CO2 stability than I have now.